LIMIT FUNGSI

A. Konsep Limit Fungsi Aljabar

Limit dapat diartikan sebagai menuju suatu batas, sesuatu yang dekat namun tidak dapat dicapai. Dalam bahasa matematika, keadaan ini dapat disebut limit. Mengapa harus ada limit? limit menjelaskan suatu fungsi jika batas tertentu didekati. Mengapa harus didekati? karena suatu fungsi biasanya tidak terdefinisi pada titik-titik tertentu. Walaupun suatu fungsi seringkali tidak terdefinisi untuk titik tertentu, namun masih dapat dicari tahu berapa nilai yang didekati oleh fungsi tersebut apabila titik tertentu semakin didekati yaitu dengan limit.

Dalam bahasa matematika, limit dituliskan dengan:

Maksudnya, apabila x mendekati a namun x tidak sama dengan a maka f(x) mendekati L. Pendekatan x ke a dapat dilihat dari dua sisi yaitu sisi kiri dan sisi kanan atau dengan kata lain x dapat mendekati dari arah kiri dan arah kanan sehingga menghasilkan limit kiri dan limit kanan.

Pengertian tentang limit di atas dapat diperoleh dengan melihat contoh berikut ini.

Untuk nilai x yang mendekati 1

Berikut gambar grafiknya:

Berdasarkan gambar grafik diatas dapat dijelaskan:

Apabila x mendekati 1 dari kiri, maka nilai f(x) mendekati 2
Apabila x mendekati 1 dari kanan, maka nilai f(x) mendekati 2
Jadi, apabila x mendekati 1, maka nilai f(x) mendekati 2

B. Sifat-sifat Limit Fungsi Aljabar

Apabila n merupakan bilangan bulat positif, k konstanta, f dan g adalah fungsi yang mempunyai limit di c, maka sifat-sifat di bawah ini berlaku.

C. Menentukan Nilai Limit Fungsi Aljabar

Ada 2 bentuk dalam menentukan limit fungsi aljabar yaitu:

Bentuk pertama

$\lim_{x\rightarrow a}f(x)$

Bentuk kedua

$\lim_{x\rightarrow \sim }f(x)$

Dalam hubungannya dengan bentuk limit yang pertama ada beberapa metode dalam menentukan nilai limit fungsi aljabar yaitu dengan cara substitusi dan cara pemfaktoran.

1. Cara Substitusi

Cara substitusi ini langkahnya dengan mengganti peubah yang mendekati nilai tertentu dengan fungsi aljabarnya. Berikut adalah beberapa contoh yang dapat dipahami.

Contoh 1:

Tentukan nilai limit fungsi aljabar dari

$\lim_{x\rightarrow 1}\ 3x-1=3(1)-1=3-1=2$

Contoh soal 2:

Tentukan nilai limit fungsi aljabar dari
$\lim_{x\rightarrow 1}\ \frac{1-x}{x+1}=\ \frac{1-(1)}{(1)+1}=\ \frac{0}{2}=\ 0$

Jadi, nilai dari limit fungsi aljabar tersebut,
$\lim_{x\rightarrow 1}\ \frac{1-x}{x+1}=\ 0$

2. Cara Pemfaktoran

Cara pemfaktoran digunakan apabila cara substitusi menghasilkan nilai limit yang tidak terdefinisikan seperti pada contoh berikut:
$\lim_{x\rightarrow 2}\ \frac{x^{2}-4}{x-2}=\ \frac{(2)^{2}-4}{2-2}=\ \frac{4-4}{2-2}=\ \frac{0}{0}$

Cara pemfaktoran dilakukan dengan langkah menentukan faktor persekutuan antara pembilang dan penyebuntya. Berikut beberapa contoh untuk dipahami.

Contoh 1:

Tentukan nilai limit fungsi aljabar dari
$\lim_{x\rightarrow 1}\frac{x^{2}+4x-5}{x-1}=\lim_{x\rightarrow 1}\frac{{\color{Red} (x-1)}(x+5)}{{\color{Red} (x-1)}}=\lim_{x\rightarrow 1}(x+5)=(1)+5=6$

Jadi, nilai dari limit fungsi aljabar tersebut,
$\lim_{x\rightarrow 1}\ \frac{x^{2}+4x-5}{x-1}=\ 6$

Contoh soal 2:

Tentukan nilai limit fungsi aljabar dari
$\lim_{x\rightarrow 3}\textup{ }\left ( \frac{x^{2}-3x}{x^{3}+2x^{2}-15x} \right )=\lim_{x\rightarrow 3}\textup{ }\frac{{\color{Red} x}(x-3)}{{\color{Red} x}(x^{2}+2x-15)}$
$\lim_{x\rightarrow 3}\textup{ }\frac{(x-3)}{(x^{2}+2x-15)}=\lim_{x\rightarrow 3}\frac{{\color{Red} (x-3)}}{{\color{Red} (x-3)}(x+5)}$
$\lim_{x\rightarrow 3}\textup{ }\frac{1}{(x+5)}=\textup{ } \frac{1}{(3)+5}=\textup{ }\frac{1}{8}$

Jadi, nilai dari limit fungsi aljabar tersebut,
$\\lim_{x\rightarrow 3}\left ( \frac{x^{2}-3x}{x^{3}+2x^{2}-15x} \right )=\textup{ }\frac{1}{8}$

Dalam hubungannya dengan bentuk limit yang kedua ada beberapa cara dalam menentukan nilai limit fungsi aljabar yaitu metode membagi dengan pangkat tertinggi penyebut dan metode mengalikan dengan faktor sekawan.

3. Metode membagi dengan pangkat tertinggi penyebut

Contoh 1:

Tentukan nilai limit fungsi aljabar dari
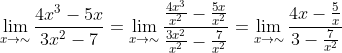
$\lim_{x\rightarrow \sim }\frac{4x^{3}-5x}{3x^{2}-7}=\lim_{x\rightarrow \sim }\frac{\frac{4x^{3}}{x^{2}}-\frac{5x}{x^{2}}}{\frac{3x^{2}}{x^{2}}-\frac{7}{x^{2}}}=\lim_{x\rightarrow \sim }\frac{4x-\frac{5}{x}}{3-\frac{7}{x^{2}}}$

Besar pangkat pembilang dan penyebut dalam soal ini adalah 3, maka
$\lim_{x\rightarrow \sim }\frac{4x-\frac{5}{x}}{3-\frac{7}{x^{2}}}=\ \frac{4(\sim )-\frac{5}{(\sim )}}{3-\frac{7}{(\sim )^{2}}}=\frac{\sim -0}{3-0}=\frac{\sim }{3}=\sim$

Jadi, nilai dari limit fungsi aljabar tersebut,
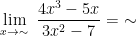
$\lim_{x\rightarrow \sim }\ \frac{4x^{3}-5x}{3x^{2}-7}=\ \sim$

Contoh soal 2:

Tentukan nilai limit fungsi aljabar dari
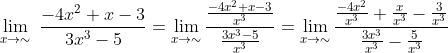
$\lim_{x\rightarrow \sim }\ \frac{-4x^{2}+x-3}{3x^{3}-5}=\lim_{x\rightarrow \sim }\frac{\frac{-4x^{2}+x-3}{x^{3}}}{\frac{3x^{3}-5}{x^{3}}}=\lim_{x\rightarrow \sim }\frac{\frac{-4x^{2}}{x^{3}}+\frac{x}{x^{3}}-\frac{3}{x^{3}}}{\frac{3x^{3}}{x^{3}}-\frac{5}{x^{3}}}$

Besar pangkat pembilang dan penyebut dalam soal ini adalah 3, maka
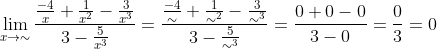
$\lim_{x\rightarrow \sim }\frac{\frac{-4}{x}+\frac{1}{x^{2}}-\frac{3}{x^{3}}}{{3}-\frac{5}{x^{3}}}=\frac{\frac{-4}{\sim }+\frac{1}{\sim ^{2}}-\frac{3}{\sim ^{3}}}{{3}-\frac{5}{\sim ^{3}}}=\frac{0+0-0}{3-0}=\frac{0}{3}=0$

Jadi, nilai dari limit fungsi aljabar tersebut,
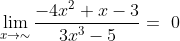
$\lim_{x\rightarrow \sim }\frac{-4x^{2}+x-3}{3x^{3}-5}=\ 0$

4. Metode mengalikan dengan faktor sekawan

Contoh soal:

Tentukan nilai limit dari

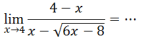
Langkah awal yang perlu dilakukan untuk menentukan nilai suatu limit yaitu dengan mensubtitusikan x=c ke f(x), sehingga dalam kasus ini substitusikan
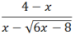
x=4 ke

Setelah disubstitusikan ternyata nilai limit tersebut tidak terdefinisi atau merupakan bentuk tak tentu

. Maka dari itu untuk menentukan nilai suatu limit harus menggunakan metode lain. Apabila diperhatikan, pada f(x) terdapat bentuk akar yaitu

sehingga metode perkalian dengan akar sekawaran dapat dilakukan pada kasus seperti ini.

Bentuk

dapat difaktorkan menjadi

Jadi, nilai limit fungsi aljabar tersebut adalah -4

D. Limit Kiri dan Limit Kanan
Limit sisi kiri dari sebuah fungsi adalah nilai yang didekati oleh fungsi tersebut apabila variabelnya bergerak mendekati limitnya melalui nilai-nilai yang membesar (x →a dari sisi kiri, melalui nilai-nilai x<a). Jadi jika

Berarti L-merupakan limit sisi kiri dari f(x) untuk x →a

Limit sisi kanandari sebuah fungsi adalah nilai yang didekati oleh fungsi tersebut apabila variabelnyabergerak mendekati limitnya melalui nilai-nilai yang mengecil (x →a dari sisi kiri, melalui nilai-nilai x>a). Jadi jika

Toerema / Pernyataan:

Suatu fungsi dikatakan mempunyai limit apabila antara limit kiri dan limit kannya mempunyai besar nilai yang sama dan apabila limit kiri dan limit kanan tidak sama maka nilai limitnya tidak ada.

E. TEOREMA LIMIT

F. BENTUK TAK TENTU

Pada limit fungsi trigonometri, telah dipelajari bahwa :

Perhatikan bentuk limit ini untuk x→0, limit pembilang dan limit penyebutnya nol. Bentuk demikian dinamakan bentuk tak tentu 0/0. Kita mengenal tujuh macam bentuk tak tentu limit fungsi, yaitu :

Pada bab ini kita hanya membahas empay bentuk yang pertama saja. Bentuk tak tentu lainnya melibatkan fungsi berpangkat fungsi, penyelesaiannya memerlukan konsep logaritma natural dan teorema L’Hospital. Permasalahan ini akan kita bahas pada penggunaan fungsi transenden dalam perhitungan limit fungsi.

Berikut dua teorema penting untuk mempelajari limit-limit tak tentu :

Berikut beberapa bentuk sekaligus contoh dalam integral tak tentu :

1.Bentuk tak tentu 0/0 :

Cara penyelesaian : Ubahlah bentuk f(x)/g(x) sehingga sifat-sifat limit fungsi dapat digunakan. Cara yang dapat dicoba adalah menguraikan pembilang dan penyebut, menggunakan rumus trigonometri, merasionalkan bentuk pecahannya, dan sebagainya.

Perhitungan limit bentuk tak tentu 0/0 diberikan dalam contoh berikut :

Contoh Bentuk 0/0 :

2. Bentuk tak tentu ∞/∞ :

Cara penyelesaian : Ubahlah bentuk f(x)/g(x) sehingga sifat-sifat limit fungsi dapat digunakan. Cara yang dapat digunakan adalah merasionalkan bentuk pecahannya, memunculkan bentuk 1/x pangkat n, n bilangan asli, dan sebagainya.

Perhitungan limit bentuk tak tentu ∞/∞ diberikan dalam contoh berikut :

Contoh Bentuk ∞/∞ :

3. Bentuk tak tentu 0.∞ :

Contoh Bentuk tak tentu 0.∞ :

4. Bentuk Tak Tentu ∞ – ∞ :

Contoh Bentuk ∞ – ∞ :

G. TEOREMA LIMIT TRIGONOMETRI

Cara menentukan nilai limit fungsi trigonometri untuk x mendekati suatu bilangan c dapat secara mudah diperoleh dengan melakukan substitusi nilai c pada fungsi trigonometrinya. Persamaan rumus limit fungsi trigonometri diberikan seperti pada gambar di bawah.
Rumus Limit Fungsi Trigonometri

Pada kasus tertentu, nilai limit untuk x mendekati bilangan 0 akan menghasilkan $\frac{0}{0}$ . Misalnya pada kasus berikut.

$\lim_{x \rightarrow 0 } \frac{sin \; x}{x}$

Jika dilakukan substitusi secara langsung, nilai limitnya adalah

$\lim_{x \rightarrow 0 } \frac{sin \; x}{x} = \frac{0}{0}$

Sebagaimana yang kita tahu bahwa nilai limit tersebut bukan nilai limit yang diharapkan. Kita perlu menggunakan metode lain untuk mendapatkan nilainya. Sekarang, simak pembahasan selanjutnya mengenai nilai limit fungsi trigonometri untnuk x mendekati 0.

Limit Fungsi Trigonometri untuk x Mendekati 0 (Nol)

Dalam pembahasan limit fungsi trigonometri, terdapat berbagai rumus yang dapat disebut sebagai “properti” untuk menyelesaikan soal limit fungsi trigonometri. Kumpulan properti tersebut dapat dilihat pada daftar rumus limit trigonometri yang diberikan di bawah.

Contoh soal limit trigonometri 1
Tentukan nilai limit fungsi trigonometri dibawah!

$\lim_{x \rightarrow 0} \frac{sin \; 3x - sin \; 2x}{4x}$

$A. \; \; \; \frac{1}{4}$

$B. \; \; \; \frac{1}{2}$

$C. \; \; \; \frac{3}{4}$

$D. \; \; \; 1$

$E. \; \; \; 1 \frac{1}{4}$

Pembahasan:

$\lim_{x \rightarrow 0} \frac{sin \; 3x - sin \; 2x}{4x} = \lim_{x \rightarrow 0} \left( \frac{sin \; 3x}{4x} - \frac{sin \; 2x}{4x} \right)$

$= \lim_{x \rightarrow 0} \frac{sin \; 3x}{4x} - \lim_{x \rightarrow 0} \frac{sin \; 2x}{4x}$

$= \frac{3}{4} - \frac{2}{4}$

$= \frac{1}{4}$

Jawaban: A

Contoh soal limit trigonometri 2
Tentukan nilai limit fungsi trigonometri dibawah!

$\lim_{x \rightarrow 0} \left( \frac{sin \; 4x}{x^{2}tan \; 2x} - \frac{2}{x^{2}} \right)$

$A. \; \; \; 8$

$B. \; \; \; 4$

$C. \; \; \; 0$

$D. \; \; \; -4$

$E. \; \; \; -8$

Pembahasan:
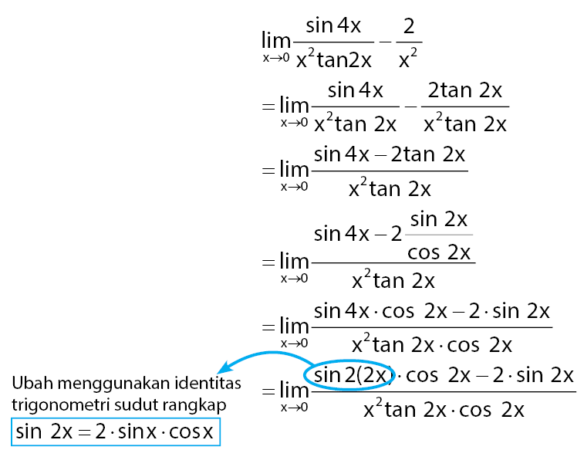
limit fungsi trigonometri

Dengan melakukan transformasi menggunakan identitas trigonometri rumus fungsi sinus sudut rangkap akan diperoleh persamaan di bawah.
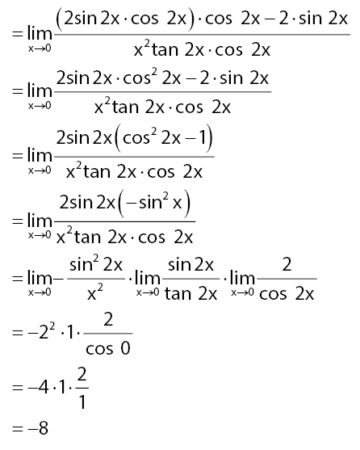
Soal limit fungsi trigonometri

Jawaban: E

Demikian penjelasan mengenai limit fungsi
Sampai jumpa di penjelasan berikutnya, terima kasih

Sumber:
https://rumushitung.com/2018/07/25/materi-limit-fungsi-aljabar/
http://file.upi.edu/Direktori/FPEB/PRODI._EKONOMI_DAN_KOPERASI/SITI_PARHAH/MATERI_4.pdf
https://elmunawarahnurdini.wordpress.com/bentuk-tak-tentu/
https://rumus.co.id/limit-trigonometri/

Cari Blog Ini

MATERI MATEMATIKA

LIMIT FUNGSI

A. Konsep Limit Fungsi Aljabar

B. Sifat-sifat Limit Fungsi Aljabar

C. Menentukan Nilai Limit Fungsi Aljabar

Ada 2 bentuk dalam menentukan limit fungsi aljabar yaitu:

2. Cara Pemfaktoran

4. Metode mengalikan dengan faktor sekawan

Contoh soal:

Toerema / Pernyataan:

G. TEOREMA LIMIT TRIGONOMETRI

Limit Fungsi Trigonometri untuk x Mendekati 0 (Nol)

Komentar

Posting Komentar

Postingan populer dari blog ini

Hubungan dan Fungsi

Matriks Lanjutan (III)