Baris dan Deret
A. PENGERTIAN BARISAN DAN DERET



rumus mencari sisipan
Jika hendak membuat sebuah baris aritmatika dengan telah diketahui nilai suku pertama (a) dan suku terakhirnya (p), dapat disisipkan sejumlah bilangan diantara keduan bilangan tersebut. Sejumlah bilangan (q buah) tersebut menjadi suku-suku baris aritmatika dan memiliki selisih antar suku beredekatan (b). Baris aritmatika tersebut memiliki jumah suku q + 2 dan diurut berupa:
Diketahui bahwa suku terakhir:
Maka, nilai b dapat ditentukan sebagai:
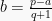
Misalkan a= 1 dan p = 9, jika disisipkan 3 bilangan diantara a dan p, maka baris belangan aritmatikanya adalah:









Demikian materi mengenai baris dan deret, semoga dapat bermanfaat
Sampai jumpa dimateri selanjutnya
sumber :
https://www.bintangwahyu.com/matematika-sma-ipa-barisan-dan-deret/
https://www.studiobelajar.com/barisan-deret-aritmatika-geometri/
1. Pengertian Barisan
Barisan adalah rangkaian bilangan yang disusun menurut aturan atau pola tertentu.
Bentuk umum barisan adalah sebagai berikut:
U1 , U2 , U3 , …. Un
Keterangan:
U1 = suku pertama
U2 = suku kedua
Un = suku ke-n
2. Pengertian Deret
Deret adalah penjumlahan suku-suku suatu barisan bilangan.
Bentuk umum deret adalah:
Sn = U1 + U2 + U3 + …. + Un
Keterangan:
Sn = jumlah n suku pertama
B. BARISAN DAN DERET ARITMATIKA
1. Barisan Aritmatika
Barisan aritmetika adalah barisan bilangan yang mempunyai beda (selisih) yang tetap/sama untuk setiap duku suku yang berurutan.
Bentuk umum barisan aritmetika adalah:
U1, U2, U3, …. , Un
a, a + b, a + 2b, …. , a + (n – 1)b
Pada barisan aritmetika terdapat beberapa rumusan sebagai berikut:
Rumus beda (b)
b = Un – Un – 1
b = U2 – U1 = U3 – U2
Rumus mencari suku ke-n
Un = a + (n – 1)b
Keterangan:
U1 = a = suku pertama/suku awal
U2 = a + b
U3 = a + 2b
U4 = a + 3b
Contoh:
Barisan aritmetika:
5, 8, 11, 14, 17, ….
Tentukan suku ke-16?
Pembahasan:
b = U2 – U1 = 8 – 5 = 3
Un = a + (n – 1)b
Suku ke – 16 adalah
U16 = 5 + (16 – 1).3
= 5 + 45 = 50
2. Deret Aritmetika
Bentuk umum deret aritmetika adalah:
U1 + U2 + U3 + …. + Un
a + a + b + a + 2b + …. + a + (n – 1)b
Pada deret aritmetika terdapat rumusan sebagai berikut:
Rumus mencari jumlah n suku pertama

Keterangan: Sn = jumlah n suku pertama
Rumus mencari suku tengah
Jika banyak sukunya ganjil maka terdapat suku tengah (Ut):
Hubungan antara jumlah n suku pertama dan suku tengah adalah:
Sn = n x Ut
Contoh:
Deret aritmetika:
4 + 10 + 16 + 22 + 28 + ….
Tentukan jumlah 20 suku pertama!
Pembahasan:

rumus mencari sisipan
Jika hendak membuat sebuah baris aritmatika dengan telah diketahui nilai suku pertama (a) dan suku terakhirnya (p), dapat disisipkan sejumlah bilangan diantara keduan bilangan tersebut. Sejumlah bilangan (q buah) tersebut menjadi suku-suku baris aritmatika dan memiliki selisih antar suku beredekatan (b). Baris aritmatika tersebut memiliki jumah suku q + 2 dan diurut berupa:
a, (a + b), (a + 2b), (a + 3b), …, (a + q.b), (a + (q+1)b)
Diketahui bahwa suku terakhir:
(a + (q+1)b) = p
Maka, nilai b dapat ditentukan sebagai:
Misalkan a= 1 dan p = 9, jika disisipkan 3 bilangan diantara a dan p, maka baris belangan aritmatikanya adalah:
- Nilai q = 3
- Jumlah suku = q + 2 = 3 + 2 = 5
- Baris aritmatika : 1, 3, 5, 7, 9
C. BARIS DAN DERET GEOMETRI
1. Baris Geometri
Bentuk umum barisan geometri adalah sebagai berikut:

Pada barisan geometri terdapat beberapa rumusan sebagai berikut:
Rumus rasio (r)
Rumus mencari suku ke-n

Contoh:
Diketahui barisan geometri:
1, 3, 9, 27, ….
Tentukan rasionya dan suku ke-7 (U7)?
Pembahasan:

2. Deret Geometri
Bentuk umum dari deret geometri sebagai berikut:

Rumus mencari jumlah n suku pertama pada deret geometri:
Contoh:
Deret geometri:
4 + 8 + 16 + 32 + …
Tentukan jumlah 9 suku pertama?
Pembahasan:

D. DERET GEOMETRI TAK HINGGA
Deret geometri tak hingga adalah deret geometri yang memiliki jumlah suku sampai tak terhingga.
Deret geometri tak hingga dibedakan menjadi:
1. Deret Geometri Divergen
Syarat deret geometri divergen: jika r < – 1 atau r > 1
Contoh:
4 + 8 + 16 + 32 + …
S∞ = ∞
S∞ = jumlah suku tak hingga
2. Deret Geometri Konvergen
Syarat deret geometri konvergen: jika –1 < r < 1
Contoh:
Maka rumus jumla suku sampai tak terhingga (S∞) adalah:

Untuk jumlah tak hingga suku-suku ganjil adalah:
Sedangkan, jumlah tak hingga suku-suku genap adalah:

Demikian materi mengenai baris dan deret, semoga dapat bermanfaat
Sampai jumpa dimateri selanjutnya
sumber :
https://www.bintangwahyu.com/matematika-sma-ipa-barisan-dan-deret/
https://www.studiobelajar.com/barisan-deret-aritmatika-geometri/

Komentar
Posting Komentar