Menyelesaikan persamaan aljabar simultan merupakan suatu proses dalam menyelesaiakan persamaan aljabar dengan metode-meode yang telah ada. Persamaan aljabar simultan sendiri adalah suatu bentuk persamaan-persamaan yang secara bersama-sama menyajikan banyak variabel bebas.

Bentuk persamaan linier simultan dengan m persamaan dan n variabel bebas dapat dituliskan sebagai berikut:

Dimana :

a i j untuk i=1 s/d m dan j=1 s/d n adalah koefisien atau persamaan simultan
x i untuk i=1 s/d n adalah variabel bebas pada persamaan simultan

Penyelesaian persamaan linier simultan adalah penentuan nilai x i
untuk semua i=1 s/d n yang memenuhi semua persamaan yang diberikan.

Persamaan linier simultan diatas dapat dinyatakan sebagai bentuk matrik yaitu:

Matrik A = Matrik Koefisien atau Matrix Jacobian
Vektor x = Vektor variabel
Vektor B = Vektor konstanta

Metode Invers Matriks (MIM)

Untuk SPLDV

Bentuk umum sistem persamaan linear dua variabel :

Dapat dinyatakan dalam bentuk matriks, yaitu :

Sehingga untuk mencari solusi dari x dan y adalah :

dengan

.
Jadi, solusi SPLDV adalah x dan y, serta Hp SPLDV = {(x,y)}.

Contoh Soal :

Nilai x yang memenuhi SPLDV

adalah …

Penyelesaian :

Sistem persamaan tersebut dapat diubah dalam bentuk matriks menjadi :

Sehingga,

Jadi Hp={(3,2)}. Sehingga nilai x yang memenuhi adalah 3.

Aturan Cramer untuk Sistem 2 × 2

Diberikan suatu sistem persamaan linear 2 × 2

maka solusinya adalah pasangan berurutan (x, y), dimana

dengan syarat D ≠ 0.

Contoh 1: Menyelesaikan Sistem Menggunakan Aturan Cramer

Gunakan aturan Cramer untuk menyelesaikan sistem berikut.

Pembahasan Pertama kita tentukan nilai-nilai dari D, Dx, dan Dy.

Sehingga kita mendapatkan

Jadi solusi dari sistem persamaan linear tersebut adalah (2, –1).

Berhati-hatilah dalam menggunakan metode ini. Sebelum menggunakan aturan Cramer, perhatikan apakah sistem yang diberikan konsisten, tidak konsisten, ataukah bergantung. Sebagai contoh,

yang apabila diubah ke dalam bentuk baku menjadi

dan memiliki determinan matriks koefisien D = (–2)(–2) – (4)(1) = 0. Karena D = 0 maka aturan Cramer tidak dapat diterapkan, dan sistem tersebut merupakan sistem yang tidak konsisten atau bergantung. Untuk mengetahui yang mana (tidak konsisten atau bergantung), kita tulis sistem tersebut ke dalam bentuk fungsi (selesaikan untuk y). Hasilnya adalah

yang menunjukkan sistem tersebut memuat dua garis sejajar dan tidak memiliki selesaian.

SPLTV Metode Invers Matriks

Dengan menggunakan metode invers matriks, tentukanlah himpunan penyelesaian dari sistem persamaan linear tiga variabel berikut ini.

2x + y – z = 1

x + y + z = 6

x – 2y + z = 0

Penyelesaian:

Pertama, kita buat nama yang spesifik dari ketiga sistem persamaan linear di atas, yaitu sebagai berikut.

2x + y – z = 1 …………… Pers. (1)

x + y + z = 6 …….……… Pers. (2)

x – 2y + z = 0 …………… Pers. (3)

Kemudian, persamaan (1), (2), dan (3) kita susun dalam bentuk matriks berikut.

AX = B

Matriks A memuat koefisien-koefisien ketiga persamaan. Matriks X memuat variabel x, y, dan z. Sedangkan matriks B memuat konstanta-konstanta ketiga persamaan linear. Dengan demikian, bentuk matriks AX = B adalah sebagai berikut.

2	1	−1	x	=	1
1	1	1	y		6
1	−2	1	z		0

Untuk menentukan nilai x, y, dan z maka bentuk matriks AX = B harus kita ubah menjadi bentuk invers seperti berikut.

AX = B

X = A-1B

Matriks dari A-1 dirumuskan sebagai berikut.

A-1 = (1/determinan A)(adjoin A)

A-1	=	1	adj	a1	b1	c1
				a2	b2	c2
		det A
				a3	b3	c3

Sampai tahap ini, kita harus menentukan nilai dari determinan matriks A dan juga adjoin matriks A. Penjelasannya adalah sebagai berikut.

Menentukan determinan matriks A

Dari matriks A tambahkan 2 kolom di sebalah kanan. Kolom keempat berisi elemen dari kolom pertama, sedangkan kolom kelima berisi elemen dari kolom kedua matriks A. Sehingga matriks A menjadi seperti berikut.

A	=	2	1	−1	2	1
		1	1	1	1	1
		1	−2	1	1	−2

Dari bentuk matrik di atas, nilai determinan dari matriks A adalah sebagai berikut.

det A = [(2)(1)(1) + (1)(1)(1) + (−1)(1)(−2)] – [(1)(1)(−1) + (−2)(1)(2) + (1)(1)(1)]

det A = [2 + 1 + 2] – [−1 – 4 + 1]

det A = 5 – (−4)

det A = 9

Adjoin matriks A

Untuk menentukan adjoin matriks A digunakan rumus berikut.

Adj A = (matriks kofaktor A)T

Jadi sebelum dapat menentukan adjoin matriks, kita harus menentukan dahulu matriks kofaktor A yang ditranspose.

Menentukan matriks kofaktor A [kof(A)]

Elemen-elemen matriks kofaktor A adalah sebagai berikut.

kof(A)	=	K11	K12	K13
		K21	K22	K23
		K31	K32	K33

Kesembilan elemen K tersebut dapat tentukan dengan menggunakan minor-kofaktor yang dirumuskan sebagai berikut.

K11 = (−1)1 + 1 M11

M11 adalah determinan minor dari matriks A yang diperoleh dengan menutup baris dan kolom pertama matriks A.

M11	=	2	1	−1
		1	1	1
		1	−2	1

M11	=	1	1	=	[(1)(1)] – [(−2)(1)]	=	3
		−2	1

Dengan demikian, nilai dari K11 adalah sebagai berikut.

K11 = (−1)1 + 1 (3) = 3

K12 = (−1)1 + 2 M12

M12 adalah determinan minor dari matriks A yang diperoleh dengan menutup baris pertama dan kolom kedua matriks A.

M12	=	2	1	−1
		1	1	1
		1	−2	1

M12	=	1	1	=	[(1)(1)] – [(1)(1)]	=	0
		1	1

Dengan demikian, nilai dari K12 adalah sebagai berikut.

K12 = (−1)1 + 2 (0) = 0

K13 = (−1)1 + 3 M13

M13 adalah determinan minor dari matriks A yang diperoleh dengan menutup baris pertama dan kolom ketiga matriks A.

M13	=	2	1	−1
		1	1	1
		1	−2	1

M13	=	1	1	=	[(1)(−2)] – [(1)(1)]	=	−3
		1	−2

Dengan demikian, nilai dari K13 adalah sebagai berikut.

K13 = (−1)1 + 3 (−3) = −3

K21 = (−1)2 + 1 M21

M21 adalah determinan minor dari matriks A yang diperoleh dengan menutup baris kedua dan kolom pertama matriks A.

M21	=	2	1	−1
		1	1	1
		1	−2	1

M21	=	1	−1	=	[(1)(1)] – [(−2)(−1)]	=	−1
		−2	1

Dengan demikian, nilai dari K21 adalah sebagai berikut.

K21 = (−1)2 + 1 (−1) = 1

K22 = (−1)2 + 2 M22

M22 adalah determinan minor dari matriks A yang diperoleh dengan menutup baris kedua dan kolom kedua matriks A.

M22	=	2	1	−1
		1	1	1
		1	−2	1

M22	=	2	−1	=	[(2)(1)] – [(1)(−1)]	=	3
		1	1

Dengan demikian, nilai dari K22 adalah sebagai berikut.

K22 = (−1)2 + 2 (3) = 3

K23 = (−1)2 + 3 M23

M23 adalah determinan minor dari matriks A yang diperoleh dengan menutup baris kedua dan kolom ketiga matriks A.

M23	=	2	1	−1
		1	1	1
		1	−2	1

M23	=	2	1	=	[(2)(−2)] – [(1)(1)]	=	−5
		1	−2

Dengan demikian, nilai dari K23 adalah sebagai berikut.

K23 = (−1)2 + 3 (−5) = 5

K31 = (−1)3+ 1 M31

M31 adalah determinan minor dari matriks A yang diperoleh dengan menutup baris ketiga dan kolom pertama matriks A.

M31	=	2	1	−1
		1	1	1
		1	−2	1

M31	=	1	−1	=	[(1)(1)] – [(1)(−1)]	=	2
		1	1

Dengan demikian, nilai dari K31 adalah sebagai berikut.

K31 = (−1)3 + 1 (2) = 2

K32 = (−1)3+ 2 M32

M32 adalah determinan minor dari matriks A yang diperoleh dengan menutup baris ketiga dan kolom kedua matriks A.

M32	=	2	1	−1
		1	1	1
		1	−2	1

M32	=	2	−1	=	[(2)(1)] – [(1)(−1)]	=	3
		1	1

Dengan demikian, nilai dari K32 adalah sebagai berikut.

K32 = (−1)3 + 2 (3) = −3

K33 = (−1)3+ 3 M33

M33 adalah determinan minor dari matriks A yang diperoleh dengan menutup baris ketiga dan kolom ketiga matriks A.

M33	=	2	1	−1
		1	1	1
		1	−2	1

M33	=	2	1	=	[(2)(1)] – [(1)(1)]	=	1
		1	1

Dengan demikian, nilai dari K33 adalah sebagai berikut.

K33 = (−1)3 + 3 (1) = 1

Sekarang kita kumpulkan semua nilai K yang diperoleh dari perhitungan di atas, yaitu sebagai berikut.

K11 = 3	K21 = 1	K31 = 2
K12 = 0	K22 = 3	K32 = −3
K13 = −3	K23 = 5	K33 = 1

Dengan demikian, bentuk dari matriks kofaktor A adalah sebagai berikut.

kof(A)	=	3	0	−3
		1	3	5
		2	−3	1

Menentukan matriks Kofaktor A Transpose [kof(A)T]

Bentuk matriks transpose diperoleh dengan cara menukar elemen-elemen baris suatu matriks menjadi elemen-elemen kolom dan menukar elemen-elemen kolom menjadi elemen-elemen baris. Dengan demikian, bentuk matriks transpose dari matriks kofaktor A adalah sebagai berikut.

[kof(A)]T	=	3	1	2
		0	3	−3
		−3	5	1

Bentuk transpose dari matriks kofaktor A merupakan matriks adjoin A, sehingga adjoin dari matriks A adalah sebagai berikut.

Adj A = (matriks kofaktor A)T

Adj A	=	3	1	2
		0	3	−3
		−3	5	1

Langkah terakhir adalah menentukan nilai x, y, dan z dengan mengubah bentuk matriks AX = B menjadi bentuk invers seperti berikut.

AX = B

X = A-1B

x	=	1	adj	2	1	−1	1
y				1	1	1	6
		det A
z				1	−2	1	0

x	=	1	3	1	2	1
y			0	3	−3	6
		9
z			−3	5	1	0

x	=	3/9	1/9	2/9	1
y		0/9	3/9	−3/9	6
z		−3/9	5/9	1/9	0

x	=	(3/9 × 1) + (1/9 × 6) + (2/9 × 0)
y		(0/9 × 1) + (3/9 × 6) + (−3/9 × 0)
z		(−3/9 × 1) + (5/9 × 6) + (1/9 × 0)

x	=	3/9 + 6/9 + 0
y		0 + 18/9 + 0
z		−3/9 + 30/9 + 0

x	=	9/9
y		18/9
z		27/9

x	=	1
y		2
z		3

Jadi, kita peroleh nilai x = 1, y = 2 dan z = 3. Dengan demikian, himpunan penyelesaian sistem persamaan linear di atas adalah {(1, 2, 3)}.

Aturan Cramer

kita punya persamaan x1 + 2x2 = 6 dan -3x1 +4x2 = 4. Biasanya kita menggunakan Metode Eliminasi atau Metode Substitusi. Tapi akan mencoba dengan cara yang sedikit berbeda yaitu dengan memanfaatkan determinan matriks, metode ini dinamakann Aturan Cramer. Metode ini untuk menyelesaikan persamaan seperti diatas atau lebih umum mencari solusi dari n persamaan dan n bilangan tak diketahui. Rumus yang akan digunakan pada Aturan Cramer ini dijamin pada teorema dibawah ini.

Teorema :

Jika AX = B adalah sistem yang terdiri dari n persamaan linier dalam n bilangan tak diketahui sehingga det(A) 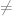$\neq$ 0, maka sistem tersebut mempunyai pemecahan yang uniq. Pemecahan ini adalah

x1 = $\frac{det(A_1)}{det(A)}$ , x2 = $\frac{det(A_2)}{det(A)}$ , …, xn = $\frac{det(A_n)}{det(A)}$

dimana Aj adalah matriks yang kita dapatkan dengan menggantikan entri-entri dalam kolom ke-j dari A dengan entri-entri dalam matriks.

B = $\left [ \begin{matrix}b_1\\ b_2\\ .\\ .\\ .\\ b_3 \end{matrix} \right ]$

Untuk lebih jelasnya, perhatikan contoh berikut ini. Carilah solusi dari persamaan dibawah ini menggunakan aturan cramer.

x1 + 2x3 = 6

-3x1 + 4x2 + 6x3 = 30

-x1 – 2x2 + 3x3 = 8

ubah terlebih dahulu kedalam bentuk matriks

A = $\left [ \begin{array}{rrr} 1& 0& 2\\ -3& 4& 6\\ -1& -2& 3\\ \end{array} \right ]$

Karena bilangan takdiketahui atau solusinya ada 3, berarti kita bentuk matriks A1, A2 dan A3. Dengan matriks A1 dibentuk dari matriks A dengan mengganti entri-entri kolom pertama pada matriks A dengan nilai-nilai pada sebelah kanan sama dengan ( = ) di persamaan diatas yaitu $\left [ \begin{array}{rrr} 6\\ 30\\ 8\\ \end{array} \right ]$ . Kemudian untuk membentuk matriks A2, kita mengganti entri-entri kolom kedua matriks A dengan $\left [ \begin{array}{rrr} 6\\ 30\\ 8\\ \end{array} \right ]$ , begitu juga untuk membentuk matriks A3 yaitu mengganti entri-entri pada kolom ketiga. Sehingga diperoleh A1, A2 dan A3 seperti dibawah ini.

A1 = $\left [ \begin{array}{rrr} 6& 0& 2\\ 30& 4& 6\\ 8& -2& 3\\ \end{array} \right ]$ , A2 = $\left [ \begin{array}{rrr} 1& 6& 2\\ -3& 30& 6\\ 8& -2& 3\\ \end{array} \right ]$ , A3 = $\left [ \begin{array}{rrr} 1& 0& 6\\ -3& 4& 30\\ -1& -2& 8\\ \end{array} \right ]$ .

Untuk menghitung determinan pada matriks A, A1, A2 dan A3 dapat menggunakan menghitung determinan menggunakan kofaktor.

det(A) = $\left [ \begin{array}{rrr} 1& 0& 2\\ -3& 4& 6\\ -1& -2& 3\\ \end{array} \right ]$

= a11C11 + a12C12 + a13C13

= a11(-1)1+1M11 + a12(-1)1+2M12 + a13(-1)1+3M13

= a11M11 – a12M12 + a13M13

= 1 $\left | \begin{array}{rr} 4& 6\\ -2& 3 \end{array} \right |$ – 0 $\left | \begin{array}{rr} -3& 6\\ -1& 3 \end{array} \right |$ + 2 $\left | \begin{array}{rr} -3& 4\\ -1& -2 \end{array} \right |$

= 1[4(3)-6(-2)] – 0[-3(3)-6(-1)] + 2[-3(-2)-4(-1)]

= 24 – 0 – 20

= 44

det(A1) = $\left [ \begin{array}{rrr} 6& 0& 2\\ 30& 4& 6\\ 8& -2& 3\\ \end{array} \right ]$

= a11C11 + a12C12 + a13C13

= a11(-1)1+1M11 + a12(-1)1+2M12 + a13(-1)1+3M13

= a11M11 – a12M12 + a13M13

= 6 $\left | \begin{array}{rr} 4& 6\\ -2& 3 \end{array} \right |$ – 0 $\left | \begin{array}{rr} 30& 6\\ 8& 3 \end{array} \right |$ + 2 $\left | \begin{array}{rr} 30& 4\\ 8& -2 \end{array} \right |$

= 6[4(3)-6(-2)] – 0[30(3)-6(8)] + 2[30(-2)-4(8)]

= 144 – 0 – 184

= -40

det(A2) = $\left [ \begin{array}{rrr} 1& 6& 2\\ -3& 30& 6\\ -1& 8& 3\\ \end{array} \right ]$

= a11C11 + a12C12 + a13C13

= a11(-1)1+1M11 + a12(-1)1+2M12 + a13(-1)1+3M13

= a11M11 – a12M12 + a13M13

= 1 $\left | \begin{array}{rr} 30& 6\\ 8& 3 \end{array} \right |$ – 6 $\left | \begin{array}{rr} -3& 6\\ -1& 3 \end{array} \right |$ + 2 $\left | \begin{array}{rr} -3& 30\\ -1& 8 \end{array} \right |$

= 1[30(3)-6(8)] – 6[-3(3)-6(-1)] + 2[-3(8)-30(-1)]

= 42 + 18 + 12

= 72

det(A3) = $\left [ \begin{array}{rrr} 1& 0& 6\\ -3& 4& 30\\ -1& -2& 8\\ \end{array} \right ]$

= a11C11 + a12C12 + a13C13

= a11(-1)1+1M11 + a12(-1)1+2M12 + a13(-1)1+3M13

= a11M11 – a12M12 + a13M13

= 1 $\left | \begin{array}{rr} 4& 30\\ -2& 8 \end{array} \right |$ – 0 $\left | \begin{array}{rr} -3& 30\\ -1& 8 \end{array} \right |$ + 6 $\left | \begin{array}{rr} -3& 4\\ -1& -2 \end{array} \right |$

= 1[4(8)-30(-2)] – 0[-3(8)-30(-1)] + 6[-3(-2)-4(-1)]

= 92 – 0 + 60

= 152

Berdasarkan Teorema diatas, maka diperoleh :