Turunan Fungsi (Lebih Dari 1 Variabel Bebas)
A. Turuna Fungsi dengan 1 Variabel Bebas
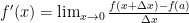 fungsi turunan juga dapat dinyatakan dengan y’ atau f’ (x) atau
fungsi turunan juga dapat dinyatakan dengan y’ atau f’ (x) atau ![[Tags] download-8-1 Rangkuman Materi Turunan Fungsi Aljabar](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bdf%28x%29%7D%7Bdx%7D&bg=ffffff&fg=000&s=0) atau
atau ![[Tags] download-8-1 Rangkuman Materi Turunan Fungsi Aljabar](https://s0.wp.com/latex.php?latex=%5Cfrac%7Bdy%7D%7Bdx%7D&bg=ffffff&fg=000&s=0)
1. Turunan Fungsi Aljabar
Berikut ini rumus turunan untuk bentuk fungsi aljabar. Rumus ini didapat dari penjabaran rumus turunan di atas.
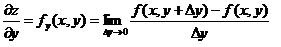
a. Fungsi dua peubah atau lebih
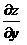
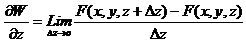
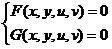
Atau ditulis dalam bentuk
Turunan fungsi ( diferensial ) adalah
fungsi lain dari suatu fungsi sebelumnya, misal fungsi f menjadi f’ yang
mempunyai nilai tidak beratuhan atauTurunan
merupakan tingkat perubahan sesaat sebuah fungsi terhadap salah satu
variabelnya. Tingkat perubahan fungsi f(x) untuk setiap nilai x, yaitu
turunan f(x), dapat dinyatakan dengan rumus:
1. Turunan Fungsi Aljabar
Berikut ini rumus turunan untuk bentuk fungsi aljabar. Rumus ini didapat dari penjabaran rumus turunan di atas.
- Jika y = k, maka y’ = 0
- Jika y = x, maka y’ = 1
- Jika
![[Tags] download-8-1 Rangkuman Materi Turunan Fungsi Aljabar](https://s0.wp.com/latex.php?latex=y%3Dx%5En&bg=ffffff&fg=000&s=0) , maka
, maka ![[Tags] download-8-1 Rangkuman Materi Turunan Fungsi Aljabar](https://s0.wp.com/latex.php?latex=y%27+%3Dn+%5Ccdot+x%5E%7Bn-1%7D&bg=ffffff&fg=000&s=0)
- Jika
![[Tags] download-8-1 Rangkuman Materi Turunan Fungsi Aljabar](https://s0.wp.com/latex.php?latex=y%3Dax%5En&bg=ffffff&fg=000&s=0) , maka
, maka ![[Tags] download-8-1 Rangkuman Materi Turunan Fungsi Aljabar](https://s0.wp.com/latex.php?latex=y%27+%3Dan+%5Ccdot+x%5E%7Bn-1%7D&bg=ffffff&fg=000&s=0)
2. KAIDAH - KAIDAH DIFERENSIAL
2. KAIDAH - KAIDAH DIFERENSIAL
1. Diferensiasi Konstanta
Jika y=k , dimana k adalah konstanta , maka dy/dx = 0
Contoh : y = 10 , maka = 0
Atau lebih mudahnya kalau kita mengganti simbol dy/dx menjadi y’ , misalnya :
y = 100 → y’ = 0
y =1/2 → y’ = 0
2. Diferensiasi Fungsi Pangkat
jika y = xn dan adalah konstanta maka dy/dx = n.Xn-1
Contoh :
1. y = x7
y’ = 7x6
2. y = x-8
y’= -8x-9
3. Diferensiasi Perkalian Konstanta dengan fungsi
Jika y=kv dan v=h(x) maka dy/dx = k dv/dx
Contoh :
-
y= 4x3 , maka dy/dx = 4 ( 3x2 ) = 12x2
-
y= 5x-8 → y’= -40x-9
-
y= 6x5 → y’ = 30x4
-
y = 3x7
y’ = 7.3x7-1
y’ = 21x6
y= 4x3 , maka dy/dx = 4 ( 3x2 ) = 12x2
y= 5x-8 → y’= -40x-9
y= 6x5 → y’ = 30x4
y = 3x7
y’ = 7.3x7-1
y’ = 21x6
4. Diferensiasi Pembagian Konstanta Dengan Fungsi
Jika y= k/v , dimana v=h(x) , maka dy/dx = k dv/dx / v2
Contoh :
-
y = 5/x3 ,
dy/dx = 5(3x2) / (x3)2
= -15x2/ x6
-
y = 4/x-8
y’= -4.-8x9 / (x-8)2
y’ = 32x-9 / x--16
y’= (32x-9). x16
y’=32x7
y = 5/x3 ,
dy/dx = 5(3x2) / (x3)2
= -15x2/ x6
y = 4/x-8
y’= -4.-8x9 / (x-8)2
y’ = 32x-9 / x--16
y’= (32x-9). x16
5. Diferensiasi Penjumlahan / pengurangan fungsi
Jika y = u ± v, dimana u = g(x) dan v = h(x) , maka dy/dx = du/dx ± dv/dx
Contoh :
y = 4x2 + x3 misalkan u = 4x2 → du/dx = 8x
v = x3 → du/dx = 3x2 , maka dy/dx = 8x + 3x2
y = -2x-1+ 4x + 8 , maka y’= 2x-2+ 4
6. Diferensiasi Perkalian Fungsi
Jika y=uv, dimana u = g(x) dan v=h(x)
Maka dy/dx= u dv/dx + v du/dx
Contoh :
- y = (4x2) (x3)
Misalkan u = 4x2 → du/dx = 8x
v = x3 → dv/dx = 3x2
Maka dy/dx = u dv/dx + v du/dx
= (4x2) (3x2) + (x3) (8x)
= 12x4+ 8x4
= 20x4
2. y = (8x2) (x4)
Misalkan u = 8x2 → du/dx = 16x
v = x4 → dv/dx = 4x3
Maka dy/dx = u dv/dx + v du/dx
= (8x2) (4x3) + (x4) (16x)
= 32x5+ 16x5
= 48x5
7. Diferensiasi Pembagian Fungsi
Jika y = U/V , dimana U = g(x) dan V=h(x)
Maka y’= VU’-UV’ / V2
Contoh :
- y = U/V → y = (4x2) / x3
y’= x3(8x) – (4x2). 3x2 / (x3)2
= 8x4-12x4 / x6
= -4x4/ x6
= -4x-2
2. y = (12x2) / x5
y’= x5(24x) – (12x2) . 5x4 / (x5)2
= 24x6 – 60x6 / x10
= -36 x6 / x10
= -36 x-4
Jika y=k , dimana k adalah konstanta , maka dy/dx = 0
Contoh : y = 10 , maka = 0
Atau lebih mudahnya kalau kita mengganti simbol dy/dx menjadi y’ , misalnya :
y = 100 → y’ = 0
y =1/2 → y’ = 0
2. Diferensiasi Fungsi Pangkat
jika y = xn dan adalah konstanta maka dy/dx = n.Xn-1
Contoh :
1. y = x7
y’ = 7x6
2. y = x-8
y’= -8x-9
3. Diferensiasi Perkalian Konstanta dengan fungsi
Jika y=kv dan v=h(x) maka dy/dx = k dv/dx
Contoh :
-
y= 4x3 , maka dy/dx = 4 ( 3x2 ) = 12x2
-
y= 5x-8 → y’= -40x-9
-
y= 6x5 → y’ = 30x4
-
y = 3x7
y’ = 7.3x7-1
y’ = 21x6
4. Diferensiasi Pembagian Konstanta Dengan Fungsi
Jika y= k/v , dimana v=h(x) , maka dy/dx = k dv/dx / v2
Contoh :
-
y = 5/x3 ,
dy/dx = 5(3x2) / (x3)2
= -15x2/ x6
-
y = 4/x-8
y’= -4.-8x9 / (x-8)2
y’ = 32x-9 / x--16
y’= (32x-9). x16
y’=32x7
5. Diferensiasi Penjumlahan / pengurangan fungsi
Jika y = u ± v, dimana u = g(x) dan v = h(x) , maka dy/dx = du/dx ± dv/dx
Contoh :
y = 4x2 + x3 misalkan u = 4x2 → du/dx = 8x
v = x3 → du/dx = 3x2 , maka dy/dx = 8x + 3x2
y = -2x-1+ 4x + 8 , maka y’= 2x-2+ 4
6. Diferensiasi Perkalian Fungsi
Jika y=uv, dimana u = g(x) dan v=h(x)
Maka dy/dx= u dv/dx + v du/dx
Contoh :
- y = (4x2) (x3)
Misalkan u = 4x2 → du/dx = 8x
v = x3 → dv/dx = 3x2
Maka dy/dx = u dv/dx + v du/dx
= (4x2) (3x2) + (x3) (8x)
= 12x4+ 8x4
= 20x4
2. y = (8x2) (x4)
Misalkan u = 8x2 → du/dx = 16x
v = x4 → dv/dx = 4x3
Maka dy/dx = u dv/dx + v du/dx
= (8x2) (4x3) + (x4) (16x)
= 32x5+ 16x5
= 48x5
7. Diferensiasi Pembagian Fungsi
Jika y = U/V , dimana U = g(x) dan V=h(x)
Maka y’= VU’-UV’ / V2
Contoh :
- y = U/V → y = (4x2) / x3
y’= x3(8x) – (4x2). 3x2 / (x3)2
= 8x4-12x4 / x6
= -4x4/ x6
= -4x-2
2. y = (12x2) / x5
y’= x5(24x) – (12x2) . 5x4 / (x5)2
= 24x6 – 60x6 / x10
= -36 x6 / x10
= -36 x-4
Jika y=k , dimana k adalah konstanta , maka dy/dx = 0
Contoh : y = 10 , maka = 0
Atau lebih mudahnya kalau kita mengganti simbol dy/dx menjadi y’ , misalnya :
y = 100 → y’ = 0
y =1/2 → y’ = 0
2. Diferensiasi Fungsi Pangkat
jika y = xn dan adalah konstanta maka dy/dx = n.Xn-1
Contoh :
1. y = x7
y’ = 7x6
2. y = x-8
y’= -8x-9
3. Diferensiasi Perkalian Konstanta dengan fungsi
Jika y=kv dan v=h(x) maka dy/dx = k dv/dx
Contoh :
-
y= 4x3 , maka dy/dx = 4 ( 3x2 ) = 12x2
-
y= 5x-8 → y’= -40x-9
-
y= 6x5 → y’ = 30x4
-
y = 3x7
y’ = 7.3x7-1
y’ = 21x6
4. Diferensiasi Pembagian Konstanta Dengan Fungsi
Jika y= k/v , dimana v=h(x) , maka dy/dx = k dv/dx / v2
Contoh :
-
y = 5/x3 ,
dy/dx = 5(3x2) / (x3)2
= -15x2/ x6
-
y = 4/x-8
y’= -4.-8x9 / (x-8)2
y’ = 32x-9 / x--16
y’= (32x-9). x16
y’=32x7
5. Diferensiasi Penjumlahan / pengurangan fungsi
Jika y = u ± v, dimana u = g(x) dan v = h(x) , maka dy/dx = du/dx ± dv/dx
Contoh :
y = 4x2 + x3 misalkan u = 4x2 → du/dx = 8x
v = x3 → du/dx = 3x2 , maka dy/dx = 8x + 3x2
y = -2x-1+ 4x + 8 , maka y’= 2x-2+ 4
6. Diferensiasi Perkalian Fungsi
Jika y=uv, dimana u = g(x) dan v=h(x)
Maka dy/dx= u dv/dx + v du/dx
Contoh :
- y = (4x2) (x3)
Misalkan u = 4x2 → du/dx = 8x
v = x3 → dv/dx = 3x2
Maka dy/dx = u dv/dx + v du/dx
= (4x2) (3x2) + (x3) (8x)
= 12x4+ 8x4
= 20x4
2. y = (8x2) (x4)
Misalkan u = 8x2 → du/dx = 16x
v = x4 → dv/dx = 4x3
Maka dy/dx = u dv/dx + v du/dx
= (8x2) (4x3) + (x4) (16x)
= 32x5+ 16x5
= 48x5
7. Diferensiasi Pembagian Fungsi
Jika y = U/V , dimana U = g(x) dan V=h(x)
Maka y’= VU’-UV’ / V2
Contoh :
- y = U/V → y = (4x2) / x3
y’= x3(8x) – (4x2). 3x2 / (x3)2
= 8x4-12x4 / x6
= -4x4/ x6
= -4x-2
2. y = (12x2) / x5
y’= x5(24x) – (12x2) . 5x4 / (x5)2
= 24x6 – 60x6 / x10
= -36 x6 / x10
= -36 x-4
Jika y=k , dimana k adalah konstanta , maka dy/dx = 0
Contoh : y = 10 , maka = 0
Atau lebih mudahnya kalau kita mengganti simbol dy/dx menjadi y’ , misalnya :
y = 100 → y’ = 0
y =1/2 → y’ = 0
2. Diferensiasi Fungsi Pangkat
jika y = xn dan adalah konstanta maka dy/dx = n.Xn-1
Contoh :
1. y = x7
y’ = 7x6
2. y = x-8
y’= -8x-9
3. Diferensiasi Perkalian Konstanta dengan fungsi
Jika y=kv dan v=h(x) maka dy/dx = k dv/dx
Contoh :
-
y= 4x3 , maka dy/dx = 4 ( 3x2 ) = 12x2
-
y= 5x-8 → y’= -40x-9
-
y= 6x5 → y’ = 30x4
-
y = 3x7
y’ = 7.3x7-1
y’ = 21x6
y= 4x3 , maka dy/dx = 4 ( 3x2 ) = 12x2
y= 5x-8 → y’= -40x-9
y= 6x5 → y’ = 30x4
y = 3x7
y’ = 7.3x7-1
y’ = 21x6
4. Diferensiasi Pembagian Konstanta Dengan Fungsi
Jika y= k/v , dimana v=h(x) , maka dy/dx = k dv/dx / v2
Contoh :
-
y = 5/x3 ,
dy/dx = 5(3x2) / (x3)2
= -15x2/ x6
-
y = 4/x-8
y’= -4.-8x9 / (x-8)2
y’ = 32x-9 / x--16
y’= (32x-9). x16
y’=32x7
y = 5/x3 ,
dy/dx = 5(3x2) / (x3)2
= -15x2/ x6
y = 4/x-8
y’= -4.-8x9 / (x-8)2
y’ = 32x-9 / x--16
y’= (32x-9). x16
5. Diferensiasi Penjumlahan / pengurangan fungsi
Jika y = u ± v, dimana u = g(x) dan v = h(x) , maka dy/dx = du/dx ± dv/dx
Contoh :
y = 4x2 + x3 misalkan u = 4x2 → du/dx = 8x
v = x3 → du/dx = 3x2 , maka dy/dx = 8x + 3x2
y = -2x-1+ 4x + 8 , maka y’= 2x-2+ 4
6. Diferensiasi Perkalian Fungsi
Jika y=uv, dimana u = g(x) dan v=h(x)
Maka dy/dx= u dv/dx + v du/dx
Contoh :
- y = (4x2) (x3)
Misalkan u = 4x2 → du/dx = 8x
v = x3 → dv/dx = 3x2
Maka dy/dx = u dv/dx + v du/dx
= (4x2) (3x2) + (x3) (8x)
= 12x4+ 8x4
= 20x4
2. y = (8x2) (x4)
Misalkan u = 8x2 → du/dx = 16x
v = x4 → dv/dx = 4x3
Maka dy/dx = u dv/dx + v du/dx
= (8x2) (4x3) + (x4) (16x)
= 32x5+ 16x5
= 48x5
7. Diferensiasi Pembagian Fungsi
Jika y = U/V , dimana U = g(x) dan V=h(x)
Maka y’= VU’-UV’ / V2
Contoh :
- y = U/V → y = (4x2) / x3
y’= x3(8x) – (4x2). 3x2 / (x3)2
= 8x4-12x4 / x6
= -4x4/ x6
= -4x-2
2. y = (12x2) / x5
y’= x5(24x) – (12x2) . 5x4 / (x5)2
= 24x6 – 60x6 / x10
= -36 x6 / x10
= -36 x-4
Jika y=k , dimana k adalah konstanta , maka dy/dx = 0
Contoh : y = 10 , maka = 0
Atau lebih mudahnya kalau kita mengganti simbol dy/dx menjadi y’ , misalnya :
y = 100 → y’ = 0
y =1/2 → y’ = 0
2. Diferensiasi Fungsi Pangkat
jika y = xn dan adalah konstanta maka dy/dx = n.Xn-1
Contoh :
1. y = x7
y’ = 7x6
2. y = x-8
y’= -8x-9
3. Diferensiasi Perkalian Konstanta dengan fungsi
Jika y=kv dan v=h(x) maka dy/dx = k dv/dx
Contoh :
-
y= 4x3 , maka dy/dx = 4 ( 3x2 ) = 12x2
-
y= 5x-8 → y’= -40x-9
-
y= 6x5 → y’ = 30x4
-
y = 3x7
y’ = 7.3x7-1
y’ = 21x6
4. Diferensiasi Pembagian Konstanta Dengan Fungsi
Jika y= k/v , dimana v=h(x) , maka dy/dx = k dv/dx / v2
Contoh :
-
y = 5/x3 ,
dy/dx = 5(3x2) / (x3)2
= -15x2/ x6
-
y = 4/x-8
y’= -4.-8x9 / (x-8)2
y’ = 32x-9 / x--16
y’= (32x-9). x16
y’=32x7
5. Diferensiasi Penjumlahan / pengurangan fungsi
Jika y = u ± v, dimana u = g(x) dan v = h(x) , maka dy/dx = du/dx ± dv/dx
Contoh :
y = 4x2 + x3 misalkan u = 4x2 → du/dx = 8x
v = x3 → du/dx = 3x2 , maka dy/dx = 8x + 3x2
y = -2x-1+ 4x + 8 , maka y’= 2x-2+ 4
6. Diferensiasi Perkalian Fungsi
Jika y=uv, dimana u = g(x) dan v=h(x)
Maka dy/dx= u dv/dx + v du/dx
Contoh :
- y = (4x2) (x3)
Misalkan u = 4x2 → du/dx = 8x
v = x3 → dv/dx = 3x2
Maka dy/dx = u dv/dx + v du/dx
= (4x2) (3x2) + (x3) (8x)
= 12x4+ 8x4
= 20x4
2. y = (8x2) (x4)
Misalkan u = 8x2 → du/dx = 16x
v = x4 → dv/dx = 4x3
Maka dy/dx = u dv/dx + v du/dx
= (8x2) (4x3) + (x4) (16x)
= 32x5+ 16x5
= 48x5
7. Diferensiasi Pembagian Fungsi
Jika y = U/V , dimana U = g(x) dan V=h(x)
Maka y’= VU’-UV’ / V2
Contoh :
- y = U/V → y = (4x2) / x3
y’= x3(8x) – (4x2). 3x2 / (x3)2
= 8x4-12x4 / x6
= -4x4/ x6
= -4x-2
2. y = (12x2) / x5
y’= x5(24x) – (12x2) . 5x4 / (x5)2
= 24x6 – 60x6 / x10
= -36 x6 / x10
= -36 x-4
Jika y=k , dimana k adalah konstanta , maka dy/dx = 0
Contoh : y = 10 , maka = 0
Atau lebih mudahnya kalau kita mengganti simbol dy/dx menjadi y’ , misalnya :
y = 100 → y’ = 0
y =1/2 → y’ = 0
2. Diferensiasi Fungsi Pangkat
jika y = xn dan adalah konstanta maka dy/dx = n.Xn-1
Contoh :
1. y = x7
y’ = 7x6
2. y = x-8
y’= -8x-9
3. Diferensiasi Perkalian Konstanta dengan fungsi
Jika y=kv dan v=h(x) maka dy/dx = k dv/dx
Contoh :
-
y= 4x3 , maka dy/dx = 4 ( 3x2 ) = 12x2
-
y= 5x-8 → y’= -40x-9
-
y= 6x5 → y’ = 30x4
-
y = 3x7
y’ = 7.3x7-1
y’ = 21x6
y= 4x3 , maka dy/dx = 4 ( 3x2 ) = 12x2
y= 5x-8 → y’= -40x-9
y= 6x5 → y’ = 30x4
y = 3x7
y’ = 7.3x7-1
y’ = 21x6
4. Diferensiasi Pembagian Konstanta Dengan Fungsi
Jika y= k/v , dimana v=h(x) , maka dy/dx = k dv/dx / v2
Contoh :
-
y = 5/x3 ,
dy/dx = 5(3x2) / (x3)2
= -15x2/ x6
-
y = 4/x-8
y’= -4.-8x9 / (x-8)2
y’ = 32x-9 / x--16
y’= (32x-9). x16
y’=32x7
y = 5/x3 ,
dy/dx = 5(3x2) / (x3)2
= -15x2/ x6
y = 4/x-8
y’= -4.-8x9 / (x-8)2
y’ = 32x-9 / x--16
y’= (32x-9). x16
5. Diferensiasi Penjumlahan / pengurangan fungsi
Jika y = u ± v, dimana u = g(x) dan v = h(x) , maka dy/dx = du/dx ± dv/dx
Contoh :
y = 4x2 + x3 misalkan u = 4x2 → du/dx = 8x
v = x3 → du/dx = 3x2 , maka dy/dx = 8x + 3x2
y = -2x-1+ 4x + 8 , maka y’= 2x-2+ 4
6. Diferensiasi Perkalian Fungsi
Jika y=uv, dimana u = g(x) dan v=h(x)
Maka dy/dx= u dv/dx + v du/dx
Contoh :
- y = (4x2) (x3)
Misalkan u = 4x2 → du/dx = 8x
v = x3 → dv/dx = 3x2
Maka dy/dx = u dv/dx + v du/dx
= (4x2) (3x2) + (x3) (8x)
= 12x4+ 8x4
= 20x4
2. y = (8x2) (x4)
Misalkan u = 8x2 → du/dx = 16x
v = x4 → dv/dx = 4x3
Maka dy/dx = u dv/dx + v du/dx
= (8x2) (4x3) + (x4) (16x)
= 32x5+ 16x5
= 48x5
7. Diferensiasi Pembagian Fungsi
Jika y = U/V , dimana U = g(x) dan V=h(x)
Maka y’= VU’-UV’ / V2
Contoh :
- y = U/V → y = (4x2) / x3
y’= x3(8x) – (4x2). 3x2 / (x3)2
= 8x4-12x4 / x6
= -4x4/ x6
= -4x-2
2. y = (12x2) / x5
y’= x5(24x) – (12x2) . 5x4 / (x5)2
= 24x6 – 60x6 / x10
= -36 x6 / x10
= -36 x-4
B. Turunan Fungsi Dua Variabel
Turunan Parsial.
Diketahui z = f(x,y) fungsi dengan dua variabel independen x dan y. Karena x dan y independen maka :
1. x berubah-ubah sedangkan y tertentu.
2 . y berubah-ubah sedangkan x tertentu.
Definisi
a. Turunan parsial terhadap variabel x
Jika x berubah-ubah dan y tertentu maka z merupakan fungsi x, Turunan parsial z = f(x,y) terhadap x sbb :
ii) Turunan parsial terhadap variabel y
Jika y berubah-ubah dan x tertentu maka z merupakan fungsi
y, Turunan parsial z = f(x,y) terhadap y sbb :
a. Fungsi dua peubah atau lebih
Fungsi dua peubah atau lebih dapat ditulis dalam bentuk
eksplisit atau implisit. Jika fungsi dua peubah dinyatakan dalam bentuk
eksplisit, maka secara umum ditulis dalam bentuk z = F(x,y). Sebaliknya
jika fungsi dituliskan dalam bentuk implisit, secara umum ditulis
dalam bentuk F(x,y,z) = 0.
Contoh:
1. z = 2x + y
2. xy + xz – yz = 0
a. Turunan Parsial Fungsi Dua dan Tiga Peubah
Misal z = F(x,y) adalah fungsi dengan variable bebas x dan y. Karena x
dan y variable bebas maka terdapat beberapa kemungkinan yaitu:
- y dianggap tetap, sedangkan x berubah-ubah.
- x dianggap tetap, sedangkan y berubah-ubah
- x dan y berubah bersama-sama sekaligus.
Pada kasus 1 dan 2 diatas mengakibatkan fungsinya menjadi fungsi satu
peubah, sehingga fungsi tersebut dapat diturunkan dengan menggunakan
definisi turunan pertama yang telah dipelajari pada kalkulus
diferensial.
Definisi
Misal
z = F(x,y) adalah fungsi dua peubah yang terdefinisi pada interval
tertentu, turunan parsial pertama z terhadap x dan y dinotasikan dengan
Untuk memudahkan persoalan andaikan z = F(x,y) maka untuk menentukan sama
artinya dengan menurunkan variabel x dan variabel y dianggap konstan
dan selanjutnya y diturunkan. Demikian pula untuk menentukan sama
artinya dengan menurukan variable y dan variable x dianggap konstant
lalu diturunkan.
Dengan
cara yang sama, andaikan W = F(x,y,z) adalah fungsi tiga peubah yang
terdefinisi dalam selang tertentu maka turunan parsial pertama
dinyatakan dengan , dan yang secara berturut didefinisikan oleh:. Differensial Total dan Turunan Total
membentuk turunan parsial dan ,perubahan dan ditinjau berasingan.sekarang kita tinjau pengaruh perubahan x dan y bersama-sama. Dalam Persamaan linier dari dan berbentuk disebut diferensial total dari z dititik 9( x,y) dan dinyatakan oleh dz :
dz =
jika z = f (x,y)mempunyai turunan parsial pertama yang kontinu di D ,maka z mempunyai diferensial total :
dz = disetiap titik (x,y) dari D
Untuk fungsi dari variabel atau lebih ,misalnya w = f ( x, y ,u ,v ) maka :
dw =
Contoh
1. tentukan dw jika w = !
penyelesaian :
dw = dx + dy - dz
2. radius dan tinggi sebuah silinder lingkaran yang tegak diukur sebagai 4 dan 10 cm ,dengan kemungkinan kesalahan pengukuran .gunakan diferensial total untuk menaksir kesalahn maksimum dalam volume yang diukur.
Penyelesaian :
Diketahui : v =
r= 4 cm
h=10 cm
dr=dh = 0,05 cm
ditanya : dv = ?
jawab :
dv = dr + dh
dv = 2 + dh
subsitusikan r = 4 ,h = 10 cm dan dr =dh = sehingga menghasilkan dv =2 (40) ( (
=
Misal z = F(x,y), dan fungsi tersebut dapat diturunkan terhadap variable x dan y, maka diperoleh turuna parisal terhadap x dan turunan parsial terhadap y yang secara berturut-turut dinotasikan dengan.
Turunan Parsial Fungsi Implisit
Fungsi Implisit 4 Peubah
BU dinyatakan denganAtau ditulis dalam bentuk
F(x,y,u,v) = 0 dan G(x,y,u,v) = 0
dengan x,y variable berpasangan dan u,v variabel
berpasangan dan F(x,y,u,v) = 0 serta G(x,y,u,v) = 0 tidak dapat berdiri
sendiri.

Komentar
Posting Komentar